
The secrets to Bermuda's Triangle...and it's Circle!
By Stephanie Britt
If we have a triangle and construct it's angle bisectors we will create the point of concurrency called the incenter. The incenter is used to create the incircle of a triangle. The incircel of a triangle is the largest circle that will fit in that triangle. We will explore the different types of incenters and incircles that we can create.
Acute triangle
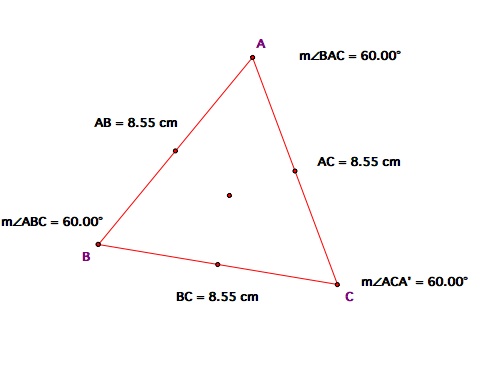
Once we create the angle bisectors we can construct the incircle of the triangle.
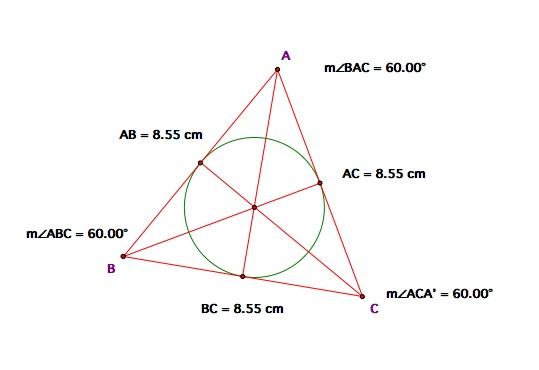
But what happens if we change the measures of the triangle such as an Isosceles Triangle or an Obtuse triangle?
Isosceles Triangle
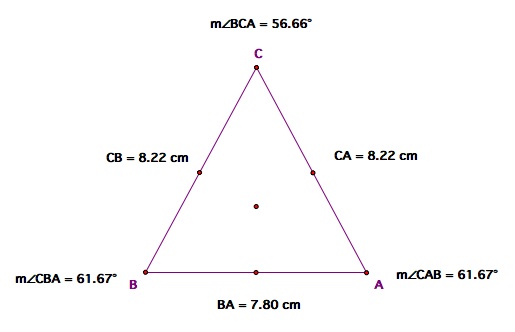
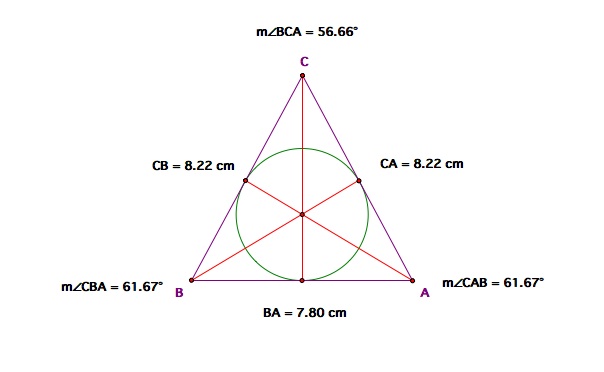
Obtuse Triangle
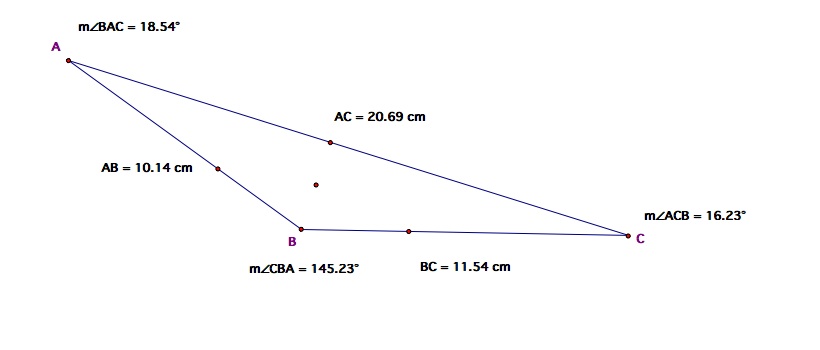
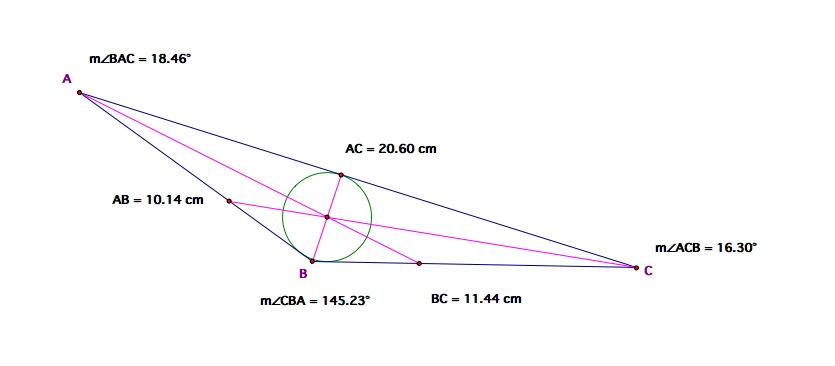
What we notice with the obtuse triangle the circle is reduced in size. It is still tangent to all three sides but it will calapse on itself as the angle of the obtuse triangle gets larger.
Could a right triangle be different?
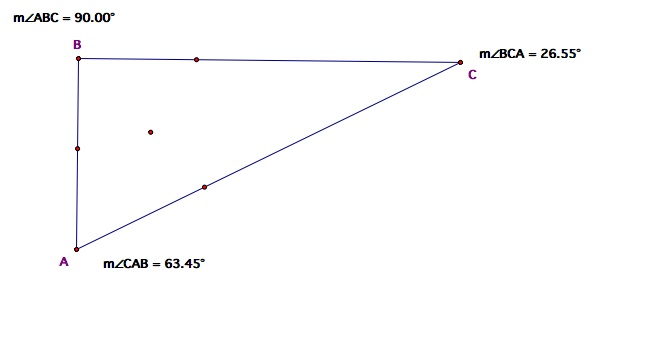
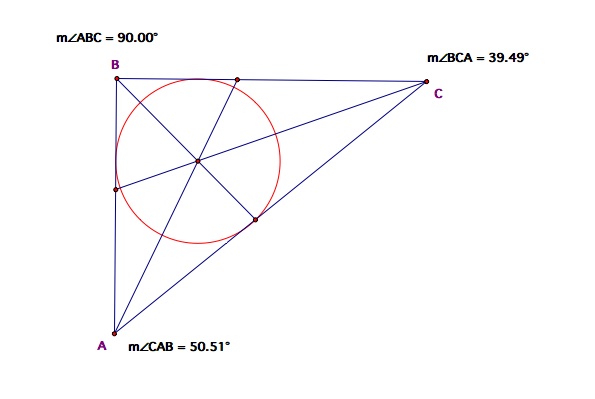
It is apparent that the circle must contain one of the intersections from the angle bisectors and the side of the triangle but it does not always contain all three. The circle contains all three points on an acute or isosceles triangle but any larger only contains one point.
You can explore the types of incircles created on your own with the scripts below.